The Mark Ortiz Automotive

CHASSIS NEWSLETTER

October 2017

Reproduction for free use permitted and encouraged.

Reproduction for sale subject to restrictions.  Please inquire for details.

Reproduction of this material elsewhere should not be construed as

an endorsement or expression of any opinion, favorable or unfavorable, by me regarding

other information appearing in the same publication, site, or medium.

WELCOME

Mark Ortiz Automotive is a chassis consulting service primarily serving oval track and road racers. This newsletter is a free service intended to benefit racers and enthusiasts by offering useful insights into chassis engineering and answers to questions.  Readers may mail questions to: 155 Wankel Dr., Kannapolis, NC 28083-8200; submit questions by phone at 704-933-8876; or submit questions by    e-mail to: markortizauto@windstream.net.  Readers are invited to subscribe to this newsletter by e-mail.  Just e-mail me and request to be added to the list.

ANTI-SQUAT WITH A TORQUE ARM AND ASYMMETRICAL TRAILING LINKS

I have been helping a friend with a Northeast 358 Dirt Modified. He has always built his own cars.

In the fall of 2015 he wanted to build one more car.  We finished it near the end of the 2016 season and ran the car 4 times.  The last race we thought we had a setup that he was happy with but had an idea of how we could improve it just a little over the winter.

The car is built with a 30 inch long torque arm with 2 radius rods.  The 2 radius rods are 31 inches long and mounted 7.5 inches below the center of the axle tubes, they can be installed at 2.5, 5, 7.5 and 10 degrees on the frame.  While running the car in 2016 we had both rods mounted at 7.5 degrees.  He felt that he had to chase the car up the track a little too much and wanted to try a longer right rear radius rod.  We installed a 45 inch long radius rod on the right but mounted it at the same height off the floor as the 7.5 degree mount for the 31 inch long rod. We started the 2017 season with the same setup as we ended 2016 except for the longer radius rod. He felt the car drove straighter but it jacked the left rear up too far on acceleration.  No matter what we did, we weren’t able to calm that jacking down.  My thought was that we messed up the anti-squat balance and were about to go back when health problems got in the way and we had to quit.  I thought I understood how to figure anti-squat with this type of suspension but when I drew it out I ran into questions, and this is why I’m writing.

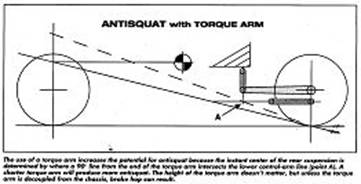
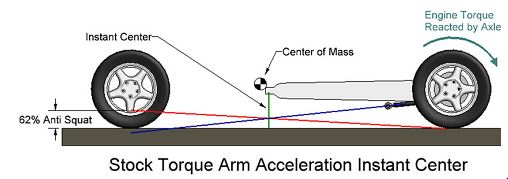
I have an article that I am attaching written by Herb Adams, I think back in the 80’s when guys, including myself, were building Reese bar torque arms, that agrees with a diagram, also attached,  I recently found on the internet of determining anti-squat with a torque arm.

I drew a quick diagram of our car, also attached, and I hope you can see what I am trying to explain on it.

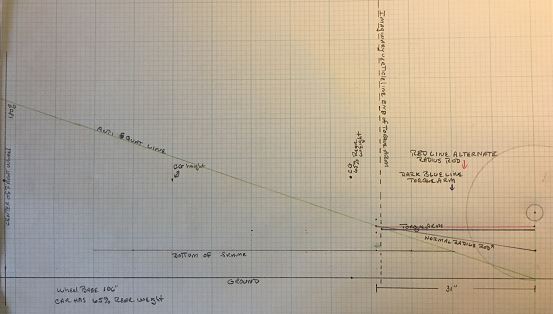
Left side geometry

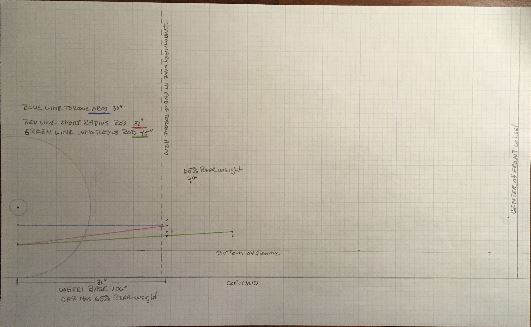
Right side geometry

The vertical line drawn through the mounting point of the torque arm falls at the same point as the front mounting point of the 31 inch radius rod.  According to the article, you draw a line from the center of the rear tire through the point where the radius rod and the vertical line intersect to a vertical line drawn through the center of the front tire.  If that point is below the center of gravity that is your percentage of anti-squat but if that point is above the center of gravity I assume that it becomes lift?  Here is my problem: on my drawing, if I leave the front mount of the radius rod the same but move the rear mount up closer to the axle tube to the point where the rod is level, according to that information, the anti-squat would be the same? There must be a way to figure how the angle of the radius rod affects the anti-squat?  It seems to me after installing the long rod that the anti-squat is as important to these cars as rear steer.  People all seem to talk about rear steer but I never hear anyone talk about anti-squat.

Could you please explain how to determine how to determine anti-squat with this type of rear suspension?

I think it is important to understand what happens when these radius rods are moved and maybe there should be more adjustments; think of all the adjustments available with the four link rear suspensions in dirt late models.  I don’t think they are just adjusting rear steer.  I know that for every action there is an equal but opposite reaction so when there is lift on acceleration there would be squat on deceleration but at the same time of backing off there is turning left.  While turning left, weight is trying to roll to the right.  With the right radius angled up towards the front, wouldn’t there be some resistance to roll created by the angled radius rod – the more the angle the more the resistance?  

The first diagram shown is correct.  The solid force line is what would give 100% anti-squat.  The dashed force line is what we get with the geometry shown, which provides about 145% anti-squat.  Point A is the effective side view instant center.

The second diagram is similar but it does contain two errors.  The effective side view instant center is where the green and blue lines cross.  The arrow doesn’t quite point there.  The red force line is drawn correctly but the percent anti-squat is mislabeled, or else the drawing is out of scale.  Scaling the graphic, I get about 43%, not 62%.

When the system has 100% anti-squat, that means the jacking coefficient is such that the induced jacking effect exactly counters the increased loading due to rearward load transfer under power, and the suspension does not compress or extend, regardless of spring rate.  When there is zero anti-squat, the increased loading is resisted entirely by the springs.  When there is 40% anti-squat, that means 40% of the load increase is resisted by the jacking force and the suspension compresses 60% as much as it would with zero anti-squat.  When there is 140% anti-squat, the suspension extends 40% as much as it would compress with zero anti-squat.  When there is 200% anti-squat, the suspension extends the same amount that it would compress with zero anti-squat.  Note that when there is more than 100% anti-squat, the rear of the car will actually sit higher under power with soft springs than with stiff ones.

We can have negative anti-squat, or pro-squat.  If we have –40% anti-squat, that means the suspension compresses 40% more under power than it would with zero anti-squat.

The related effect under braking is called anti-lift.

With a beam axle, the two-dimensional, side view geometry methods shown in the illustrations are only valid when the system is symmetrical.  When the system is slightly asymmetrical, as in a road car with a bit of roll displacement, the 2D method is still a fairly close approximation.  When we have a beam axle with pronounced asymmetry, for good accuracy we need a more complex approach.

With a torque arm and two trailing links, we have jacking forces acting on the frame at three points.  We have compression loads on the two trailing links, which are transmitting the thrust from the axle assembly to the frame.  If these are not horizontal, each one induces a vertical force equal to the thrust force at that link times the slope of the link.  The links are inboard of the wheels, so each link reacts some of the thrust from each tire, but each link reacts more of the thrust from the near tire than from the far one.  With a locked axle, the thrust from the two tires can be very unequal, and can often be negative at one tire.  Roll moments resulting from the link jacking forces will then vary dramatically depending on the distribution of thrust from the two tires.  However, we can assume for simplicity that the thrust forces are approximately equal when we’re experiencing wheelspin on dirt, although when we’re cornering at the same time there will probably be more thrust from the outside tire than from the inside one due to the outside tire having more load on it.

It will be apparent that the link jacking effects are inextricably related to roll steer.  When we add roll oversteer by putting slope in either of the links, we also add anti-squat, mainly on the side we change.

The torque arm exerts only a lifting force, because it has a slider or a drop link at its front end and can’t react thrust.  The torque creating the lifting force is not necessarily equal to the axle torque when the trailing links are below the axle (or above it).  The torque is equal to the combined moments of the two contact patch thrust forces acting about an axis of rotation.  That axis of rotation is defined by the rear pivots of the trailing links when those are directly under the axle, or the two points where the link centerlines intersect the vertical axle plane (YZ plane containing the axle centerline).  This torque divided by the torque arm length is the lifting force at the torque arm.

The total lifting force, divided by the load increase due to sprung mass rearward load transfer, times 100%, is the overall percent anti-squat.

When the car has four trailing links and two birdcages, as in a dirt Late Model, each combination of a birdcage and two links acts like a single link with one pivot at axle center and the other at the side view instant center defined by the links.

In the questioner’s example, where the links and the torque arm have nearly equal length, raising the rear of the links reduces the jacking force from the links but increases the jacking force from the torque arm.  Lowering the front of the links reduces the link jacking force without affecting the force from the torque arm.  Lengthening a link while leaving the front at the same height, as on the right side of the questioner’s car, reduces anti-squat and anti-lift on that side of the car.

To reduce rear steer without increasing torque roll, and without reducing overall anti-squat, we could raise the rear of both links.  Or, we could level out both links by moving the front down or forward, but that would reduce overall anti-squat.

With any car, there is a simple way (in theory at least) to measure the jacking coefficient for propulsion, braking, or cornering for any wheel.  I have mentioned this in the past.  If we can measure how much the contact patch moves longitudinally (x axis, propulsion or braking) or laterally (y axis, cornering) per inch of suspension travel, we know the jacking coefficient for that mode.  For propulsion, the wheel must be locked at the engine (car in gear, engine off).  For braking, the wheel must be locked with the brakes.  With a beam axle, we need to move both wheels at once.  In many cases, the jacking coefficient will be different for braking and for propulsion.  In the suspension we’re discussing here, they will be the same.

For example, if the bottom of the tire moves rearward as the suspension compresses at a rate of a tenth of an inch per inch of suspension travel, we have a 1:10 jacking coefficient.  The force line has a slope of one in ten and the system generates one pound of jacking force for each ten pounds of thrust at the tire.

For propulsion with rear wheel drive, the percent anti-squat is the jacking coefficient times the wheelbase divided by the sprung mass center of gravity height, times 100%.  For braking, the percent anti-lift is

the jacking coefficient, times the wheelbase divided by the sprung mass c.g. height, times the percentage of braking done by the rear wheels.