The Mark Ortiz Automotive
CHASSIS NEWSLETTER
Presented free of charge as a service
to the Motorsports Community
September/October2003
WELCOME
Mark Ortiz Automotive is a chassis consulting service primarily serving oval track and road racers. This newsletter is a free service intended to benefit racers and enthusiasts by offering useful insights into chassis engineering and answers to questions. Readers may mail questions to: 155 Wankel Dr., Kannapolis, NC 28083-8200; submit questions by phone at 704-933-8876; or submit questions by e-mail to: markortiz@vnet.net. Readers are invited to subscribe to this newsletter by e-mail. Just e-mail me and request to be added to the list.
SHOCK RESEARCH UPDATE
Regular readers will recall that I am coordinating an effort to investigate sensitivity of dampers to factors other than velocity, including acceleration and jerk. I still have a long way to go on this, and am still seeking persons to contribute shocks for test, especially shocks that dyno similarly in standard crank dyno testing but behave differently on the track.
I have been able to learn a little already, however, and I would like to relate these findings.
When I look at dyno output for a shock, I like to look at a force-versus-absolute-velocity trace for the full stroke: both the rebound-closing/compression-opening (extended) end and the compression-closing/rebound-opening (compressed) end. Such a trace will have two “noses” or points at the left side of the graph, each having its vertex at the zero-velocity point. Another way of displaying the information is a force-versus-velocity plot. This will generally take the form of an S-shaped loop, which will cross the zero-velocity line at two distinct points. The force-versus-absolute-velocity trace is just the force-versus-velocity trace, with the negative-velocity part of the trace folded over to the positive side because the velocities are being expressed as their absolute rather than signed values.
Almost invariably, the zero-velocity point for the cc/ro trace will be higher (indicating greater extension force) than the rc/co trace.
When the shock is cycled very slowly, if it has any bleed or leakage at all past the piston, and especially if we hold the shock stationary at the ends of the stroke and let the force readings stabilize, we will get a reading of the gas spring effect. We should expect the two nose points to be separated by this amount even in the absence of acceleration sensitivity or other effects.
The appearance of a loop-shaped force-versus-velocity trace has led some writers to call the effect hysteresis. This may or may not be strictly correct, depending on exactly how we define the term, and how meticulous we want to be. My Webster’s dictionary defines hysteresis as “a retardation of the effect when the forces acting upon a body are changed (as if from viscosity or internal friction)”.
My dictionary traces the etymology of the word to the Greek verb hysterein, meaning to be late or fall short.
How does this relate to what dampers do, or to what we’d like them to do? I think it’s pretty safe to say that we want a damper to generate a force opposing motion of the suspension at all times. How big this force should be, in what circumstances, is less certain. But we can at least say that if the damper is generating a force in the same direction as the system is moving, the damper is exaggerating motion rather than damping it, for as long as this state of affairs prevails. A suspension system in such a condition is sometimes said to be self-exciting, which is the opposite of damped.
I am not saying that damper opposition to motion is always optimal for roadholding – merely that this is what damping means. And the shock, being a passive mechanical device, cannot be expected to know when damping is desirable. All we can reasonably expect a damper to do is damp motion, and do so in some consistent manner with respect to velocity, acceleration, and jerk of its sprung and unsprung elements.
Note that motion, force, and force change are different from each other. Actually, viscosity does not always retard response to a change in force as the dictionary’s language would suggest. Sometimes it exaggerates response to a change in force – so even my dictionary doesn’t make perfect sense. For example, suppose we have a system damped by an ideal viscous fluid (totally incompressible and non-volatile). Suppose the system is in motion, and the force moving it is diminishing or reversing, and the motion is slowing. The damping force will oppose the motion, and therefore hasten the slowing – meaning the viscosity is actually hastening response to the force change, not retarding response.
So when we discuss the meaning of “hysteresis”, we confront a situation where even those charged with defining the term have an imperfect grasp of the phenomena the term attempts to describe. Does hysteresis mean damping? If we’re talking about rubber, it does. Does it mean a response lag in damping? Maybe, as some people apply it to shocks. But clearly then it does not mean damping. It may even imply temporary absence of damping, or anti-damping – behavior more like a spring than a damper. But would we speak of an ideal spring (no self-damping or non-linearity) as having hysteresis? Not ordinarily.
Engineers tend to think of hysteresis as anything that produces a loop-shaped data trace when a system is subjected to forced oscillation. But of course the meaning of this will depend on what variables we’re plotting. The earliest shock dynos generated a force-versus-displacement plot. For a damper that’s working reasonably well, this will always be a loop, typically shaped something like an egg, and sometimes called an egg plot. More modern dynos, including crank dynos with continuous computerized data acquisition, can also produce an egg plot.
Looking at such a plot, we may say we’re seeing a hysteresis loop. A shock is supposed to have hysteresis in this sense. It won’t do its job if it doesn’t.
An ideal spring should produce a force-versus-displacement plot that’s a straight line – or actually two straight lines, overlaid.
A spring is not a velocity-sensitive device, but in a sinusoidal test, we have a fixed relationship between velocity and displacement. Therefore, we know the velocity at any given displacement, and we can create a force-versus-absolute-velocity trace or a force-versus-velocity trace based on that. For an ideal spring, the force-versus-absolute-velocity trace will be half of a sine curve, stood on its side, or an arcsine curve for half a period – or, more precisely, two such traces, overlaid. That trace may be regarded as having two “noses” at the zero-velocity line or vertical axis, rather like what we see with many shocks. The force-versus-velocity trace will be the same, only with the negative-velocity trace folded over to the left side of the vertical axis instead of overlaid on the positive-velocity trace. That gives a loop-shaped trace, resembling an ellipse, although mathematically not a true ellipse.
So an ideal damper, with nothing in it that acts like a spring, produces a loop-shaped force-versus-displacement trace, and produces a force-versus-velocity trace that is not a loop but rather two curves overlaid. Its force-versus-absolute-velocity plot is likewise two traces overlaid. The force-versus-velocity and force-versus-absolute-velocity plots have only one zero-velocity point.
Conversely, an ideal spring produces no loop in its force-versus-displacement trace, but produces a big loop in its force-versus-velocity trace, and two widely-spaced noses in its force-versus-absolute-velocity trace, which is two traces overlaid.
A device that acts as both a spring and a damper will produce loop-shaped traces for both force-versus-displacement and force-versus-velocity. Other effects may also produce a loop-shaped force-versus-velocity trace.
In an automotive suspension damper, we can get spring effects from both the gas spring and other compliances, primarily compressibility of the fluid.
What we see when testing some – but not all – shocks is that the noses are separated by a greater amount than gas spring effect alone can account for. We also sometimes see that the nose separation tends to increase as the valving gets stiffer. This is particularly easy to see when dynoing certain adjustable shocks at a series of settings: as you stiffen the damping, the noses spread further apart.
Also, in some cases, the noses spread further apart when the shock is cycled faster, with stroke unchanged. In such a case, we are looking at an unchanged shock, but greater velocities, accelerations, and jerks.
What my collaborators have done to date is to test single-tube, deflective-disc shocks at twice the usual frequency and half the usual stroke (1” stroke, 3.2 Hz rather than 2” and 1.6 Hz), and also test
them upside down. So far, these tests have not been done on shocks with other types of valving, or on low-pressure, twin-tube gas shocks.
The results have more or less confirmed what the appearance of a deflective-disc valve suggests: this type of valving is not highly acceleration-sensitive. The discs do have some inertia, of course, so this was not entirely a foregone conclusion.
When a typical stock car shock, with reasonably soft valving and some bleed, is tested upside down, the forces it generates do not change noticeably. When the shock is body-up, as it’s usually installed, the piston and discs are subjected to accelerations. When the shock is body-down, the body moves instead, and the piston and discs have a constant velocity of zero – therefore no acceleration or jerk. When the shock dynos the same both ways, that implies that, at least within the range of accelerations present in the test, the shock is not acceleration-sensitive.
Also, when typical stock car shocks are tested at half the stroke and double the frequency, that generally does not have much effect on the forces. Compared to the standard test, this test produces identical velocity at any given crank angle or point in the cycle, but twice the acceleration and four times the jerk. The lack of much effect on forces in this test suggests that, at least for relatively moderate acceleration and jerk values, the shock is a predominantly velocity-sensitive device.
The finding that many dampers are not truly acceleration-sensitive is not a setback. The important thing is that we have a test for this, and therefore we can separate true acceleration sensitivity from other effects that may make a damper act different at the compressed and extended end of its stroke, and act different when cycled at differing speeds or adjustment settings. I would like to explore some such effects here.
I am adding some six shock dyno graphs to this newsletter. Three of them are on pages 6, 7 and 8. The other three are separate attachments. These last three are Adobe pdf files. You will need Adobe Acrobat to open them. An Adobe Acrobat reader is available free at www.adobe.com.
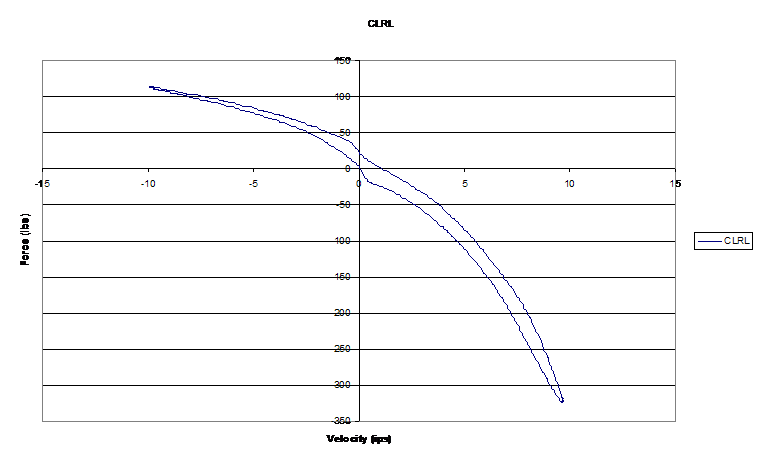
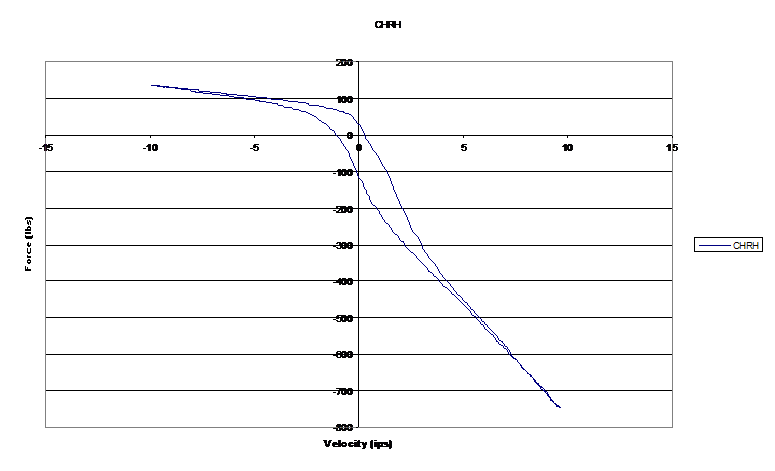
The first two plots are from a mountain bike shock used on a Formula SAE car. This is a deflective-disc shock. It has relatively little bleed, judging by the lack of a soft, progressive region at low absolute velocities. This shock is adjustable, and the plots are for a soft setting on both compression and extension, and a stiff setting on both compression and extension. The test is the same in both cases: 1” stroke, 200 rpm. This shock is so small that it can’t be tested at 2” stroke and 100 rpm. It doesn’t have 2” of stroke. Consequently, the only way to get the absolute velocity up to the 10 in/sec customary in race car shock testing, using a crank dyno, is to turn the crank faster than customary.
The first two pdf files are from Bilstein stock car shocks, with valving codes 5030 and 7030. Plots were furnished by Bilstein’s Mooresville, North Carolina facility. These are full-size, non-adjustable shocks, also with deflective-disc valving. I chose these for comparison with the mountain bike shock because they generate roughly similar forces around 4 to 5 in/sec, but they have much more piston
area (hence lower working pressures) and more bleed, as indicated by the relatively soft and progressive behavior at low absolute velocities.
Now consider the zero-velocity points on these four plots. The ones on the soft mountain bike and soft stock car shock are separated by very similar amounts: about 20 lb. However, the zero-velocity points on the stiffer stock car shock are separated by about 30 lb., while those on the stiff mountain bike trace differ by at least 130 lb. The spread on the small shock with high working pressure and little bleed grew much more as the damping was stiffened.
The third pdf file is from an 8060 Bilstein. It is stiffer at 4-5 in/sec than either of the two mountain bike calibrations shown. Yet it also shows relatively little spread at the zero-velocity points. Big piston; substantial bleed; still not much spring-like behavior.
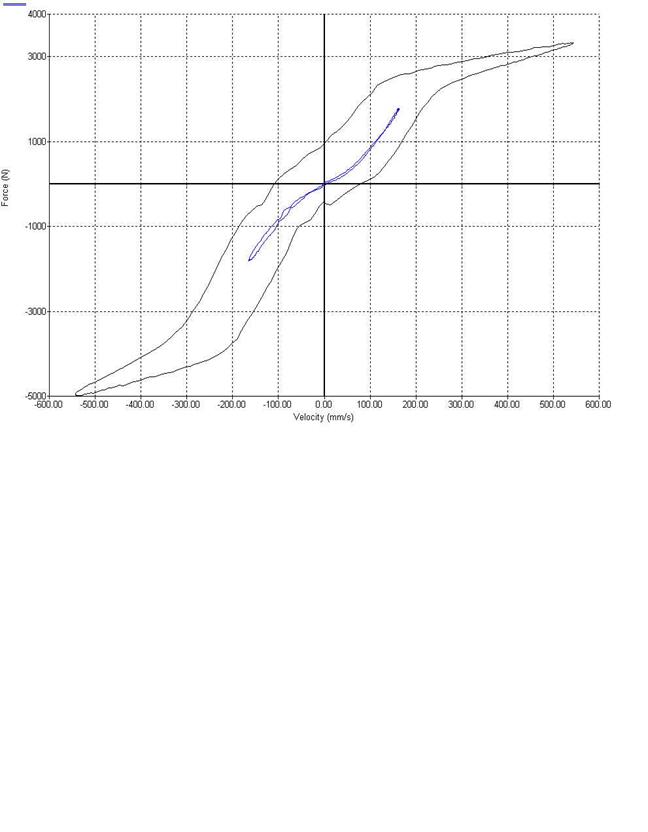
The plot on page 8 is from a correspondent at Bilstein’s Australia headquarters. It shows a shock of specifications unknown to me, tested two different ways with no changes to the shock. The Bilstein 8060 appears to be similar, although perhaps a bit softer at high speeds. The 8060 is considered a stiff shock by stock car standards, so the Australian shock is definitely stiff by stock car standards. Yet the progressive character at low speeds suggests it has similar bleed and preload to the 8060.
The plot from Australia is different from what most Americans will be used to looking at, in two obvious ways. First, the sign conventions for the velocity are reversed. (This is because the dyno is in the southern hemisphere and therefore upside down – no, not really; it’s because these sign conventions are arbitrary and the choice is up to the dyno manufacturer.) Second, the units are metric. Handy conversion factors:
1” = 25.4 mm
1 mm = approx. .04 in
100 mm/sec = approx. 4 in/sec
200 mm/sec = approx. 8 in/sec
300 mm/sec = approx. 12 in/sec
400 mm/sec = approx. 16 in/sec
500 mm/sec = approx. 20 in/sec
1 Newton = approx. .225 lbf
1 lbf = approx. 4.45 N
1000 N = approx. 225 lbf
2000 N = approx. 450 lbf
3000 N = approx. 675 lbf
4000 N = approx. 900 lbf
5000 N = approx. 1125 lbf
I am told that the Australian shock was tested at the same stroke, at two different rpm’s. The smaller trace appears to have been done at 30% the speed of the larger one. Applying the above conversion factors, if the stroke was 50 mm, which is close to the 2” common in shock testing, the rpm’s would have been about 60 and 200. So compared to the standard 2” stroke, 100 rpm test, we are looking at a considerably lower-speed test, and one about twice as fast.
In the low-speed test, the trace shows almost no spring effect. We very nearly have two identical traces overlaid – hardly a loop at all. The medium-speed 8060 test, shown in force-versus-velocity format, would be only slightly more of a loop. But double that speed, with more high-speed damping thrown in, and we see a really fat loop. This indicates that even a shock with generous piston size and significant bleed starts to act like a spring if the speeds and forces get high enough.
Okay – what conclusions can we draw? One would be that when we set out to investigate a particular phenomenon, we may stumble upon others we weren’t looking for. Nothing new here; many of the greatest discoveries in science were accidentally made this way.
Another is that end-of-stroke phenomena include not only acceleration sensitivity but effects related to entrapment and compressibility of the damping fluid – and possibly some deflections of other components. These effects are not readily separable from acceleration sensitivity, although testing the shock upside down can tell us quite a bit. Of course, not all shocks can be tested upside down.
Finally, it appears that it is highly desirable to be able to create tests that vary acceleration and jerk in mid-stroke, without altering velocity. This will involve exploiting the capabilities of recently introduced linear-motor dynos.