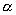 , y = r1 cos
, y = r1 cos 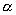 . The following sketch illustrates:
. The following sketch illustrates:In the previous instalment, we did exact calculations for a dummy line down a 650-foot entry straight, a 180-degree left-hander, and a 650-foot exit chute. Cornering radii vary from 150 feet to 200 feet, and the track is 100 feet wide all the way around. This dummy line carries constant speed around the entire left-hander. We did those calculations to provide reference times to compare against this month's more sophisticated calculations, in which we unwind the steering wheel and accelerate at the same time. The baseline times for the dummy line over the whole course, as a function of cornering radius, are in the second-to-last column of the following table:
| Inscribed Corner Radius (ft) | Total time (sec) up to the apex | Time (sec) in corner after apex | Time for entrance and complete corner | Exit speed from chute (mph) @ g/2 accel | Time in exit chute (sec) | Combined segment time | Combined post-apex time and exit-chute time |
|---|---|---|---|---|---|---|---|
| 150 | 11.872 | 0.000 | 11.872 | 109.091 | 5.670 | 17.541 | 5.670 |
| 152 | 10.912 | 0.860 | 11.773 | 107.857 | 5.528 | 17.301 | 6.388 |
| 154 | 10.544 | 1.209 | 11.754 | 107.422 | 5.460 | 17.213 | 6.669 |
| 155 | 10.401 | 1.348 | 11.750 | 107.260 | 5.430 | 17.180 | 6.779 |
| 160 | 9.872 | 1.881 | 11.753 | 106.697 | 5.308 | 17.061 | 7.189 |
| 170 | 9.208 | 2.600 | 11.808 | 106.101 | 5.116 | 16.924 | 7.716 |
| 180 | 8.762 | 3.126 | 11.888 | 105.806 | 4.955 | 16.844 | 8.082 |
| 190 | 8.424 | 3.556 | 11.980 | 105.666 | 4.813 | 16.792 | 8.369 |
| 200 | 8.150 | 3.927 | 12.077 | 105.627 | 4.682 | 16.760 | 8.609 |
From this point on, we need only look at the last column. It's after the apex and down the exit chute where we look for improvement we actually drive the dummy line up to the apex. Many readers will be screaming that we could try to get on the gas before the apex for even more improvement. Others will be screaming " trail brake!," that is, ease off the brakes at the same time as winding the steering wheel at turn in (thanks to reader Marc Sibilia for pointing this out to me). We leave those refinements to later articles.
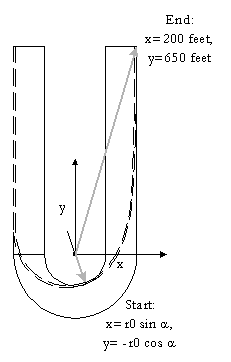
The approach in this article is to find a line by building it up, step-by-step, honouring the traction circle and the sides of the track. This is one of the techniques we can use in computer simulations, so we get to kill two birds with one stone: previewing simulation and analysing a particular driving line. For convenience, we need a Cartesian coordinate system, that is, a square grid. Let's turn the track around 180 degrees for this purpose, and put the centre of the coordinate system at the centre of the corner. Since the inside edge of the track and the outside edge of the track are concentric semicircles, there is only one identifiable centre of the corner.
We'll work by measuring the position and heading of the centroid of the car
with respect to this new coordinate system. We have a goal of arriving at the
point x = 200, y = 650,
measured in feet, in the least possible time, with a heading of as close to 90
degrees as we can get it, that is, heading straight down the track. We start at
the apex, which measures from x = r0 sin 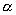 , y = r1 cos
, y = r1 cos 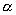 . The following sketch illustrates:
. The following sketch illustrates:
I must note, at this point, if you haven't already noticed, this instalment of The Physics of Racing is going to be more concentrated and intense than previous instalments. I'm just going to blurt out facts without the usual explanations and walkthroughs. The reasons are (1) that we have a lot to get through in a little space and (2) that we assume that if you've been following the series this far, you've got the fortitude to work through it. So, let's get it on!
The initial heading is tangent to the inner edge of the track, that is,
perpendicular to the line from the centre of the track's corner to the apex.
Therefore, it has the angle  up from the horizontal x axis.
We know the starting speed, v0, so we know its components in
the x direction and in the y direction: v0x = v0 cos
up from the horizontal x axis.
We know the starting speed, v0, so we know its components in
the x direction and in the y direction: v0x = v0 cos  , v0y = v0 sin
, v0y = v0 sin  .
.
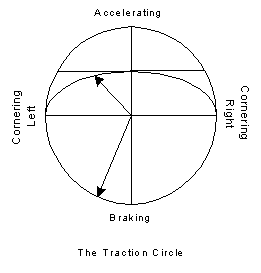
We perform the entire manoeuvre whilst never exceeding the limits of the traction circle. We set those limits as 1g cornering and braking and 0.5g accelerating, with smooth transitions all way around, as in the following sketch (the horizontal cap shows a way of accounting for engine limitations with non-smooth transitions, which will allow us to accelerate harder with the wheel still turned but probably scare us in the seat. Also, we note that 0.5g is a plausible, if only approximate, number for acceleration. We leave it to the reader to show that 0.5g in the quarter mile results in a realistic 13-second elapsed time, if at an unrealistic speed of 150 mph):
In each step of the calculation, we keep track of the following information:
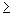 650)
650)
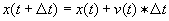 , and likewise for y
, and likewise for y
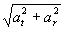 is inside the traction envelope
is inside the traction envelope
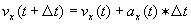 , and likewise for vy
, and likewise for vy We drive the whole simulation by feeding on the throttle linearly with time over a time span called k and by simultaneously increasing the instantaneous radius of the driving line over a potentially different time span called kunwind. Feeding on the throttle allows us to increase the tangential acceleration, at at each time step, and unwinding allows us to decrease the radial acceleration, ar so we can stay within the traction circle. Since we'll still have centripetal traction available after the throttle is buried full on, we ought to be able to unwind more slowly, enabling us to stay on the track, but use it all up. In other words, we ought to look for solutions wherein kunwind is larger than k, perhaps by twice.
Let's look at the first few rows of this simulation in a spreadsheet and delve into the formulas more deeply:
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| t | a(t) (tangential, fpsps) | v2/r (radial, fpsps) | a(t) (radial, fpsps) | r(t) (feet) | ax(t) (fpsps) | ay(t) (fpsps) | x(t) (feet) | y(t) (feet) | vx(t) (mph) | vy(t) (mph) | v (mph) |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 0.00 | 0.00 | 32.00 | 32.00 | 160.00 | -21.33 | 23.85 | 66.67 | -74.54 | 36.36 | 32.52 | 48.79 |
| 0.20 | 1.28 | 31.90 | 30.27 | 169.92 | -21.20 | 21.64 | 76.80 | -64.41 | 33.46 | 35.66 | 48.90 |
| 0.40 | 2.56 | 31.59 | 28.54 | 182.30 | -20.76 | 19.75 | 86.09 | -53.42 | 30.59 | 38.51 | 49.18 |
| 0.60 | 3.84 | 31.06 | 26.81 | 197.64 | -20.06 | 18.19 | 94.54 | -41.64 | 27.79 | 41.12 | 49.63 |
| 0.80 | 5.12 | 30.32 | 25.08 | 216.59 | -19.17 | 16.96 | 102.20 | -29.13 | 25.10 | 43.54 | 50.25 |
| 0.90 | 5.76 | 29.85 | 24.22 | 227.68 | -18.67 | 16.47 | 105.74 | -22.62 | 23.80 | 44.69 | 50.63 |
| 1.00 | 6.40 | 29.33 | 23.35 | 240.01 | -18.13 | 16.05 | 109.09 | -15.94 | 22.53 | 45.80 | 51.04 |
[column 1]: increments 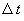 by each row we actually computed with
by each row we actually computed with 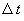 = 0.05 sec and display here every
fourth actual row this is an independent column, meaning that it does not
depend on data from any other column.
= 0.05 sec and display here every
fourth actual row this is an independent column, meaning that it does not
depend on data from any other column.
[column 2]: tangential acceleration,
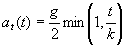 ,
,
accounting for squeezing on the throttle up to g / 2 depends only on column 1.
[column 3]: maximal radial acceleration,
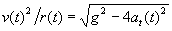 ,
,
accounting for the traction circle more precisely, for the upper half of the circle treated as a flattened (oblate) ellipse with height g / 2 depends only on column 2.
[column 4]: radial
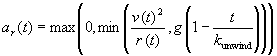 ,
,
accounting for unwinding the steering wheel in steps from the inner parentheses outwards: g(1 - t / kunwind) slowly decreases from g as time increases from 0, but, it is never allowed to exceed v2 / r, by the min expression, as mandated by the traction circle, and then, never allowed to be negative, by the max expression, because we don't want to start turning back toward the entry straight depends on columns 1 and 3.
[column 5]:
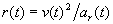
just for amusement, it's interesting to calculate the instantaneous radius of a circle we could be driving if we were not accelerating tangentially depends on columns 4 and 12, but no other columns depend on this.
[column 6]:
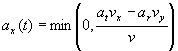 ,
,
this just selects out the x components of both the radial and tangential accelerations, but makes sure that we never turn the wheel so much that we start going to the left. Note that the radial acceleration always tries to pull the car to the left, hence the minus sign (centripetal: see part 4 of The Physics of Racing) depends on columns 2, 4, 10, 11, and 12.
[column 7]:
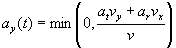 ,
,
selecting the y components, this time always pointing down the track, the way we want to go depends on columns 2, 4, 10, 11, and 12.
[column 8]:
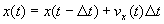 ,
,
just update the x coordinate by the velocity from the prior time step depends on columns 8 (the prior row of itself) and 10.
[column 9]:
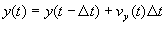 ,
,
do likewise for the y coordinate depends on columns 9 (prior row) and 11.
[column 10]:
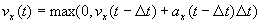 ,
,
for updating the x component of the velocity (but don't let it go negative, checking yet again, and, yes, this is a hack) depends on columns 10 (prior row) and 6.
[column 11]:
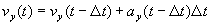 ,
,
likewise for the y coordinate of the velocity depends on columns 11 and 7.
[column 12]: finally,
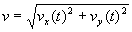 ,
,
depends on columns 10 and 11.
I've packed all this in an Excel spreadsheet. The spreadsheet should be in the download package for readers who acquired this document electronically.
Enough talk! Let's drive! Driving means playing with the values of r, k, and kunwind,
and possibly even 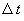 , to find the lowest overall time at which
columns 8 and 9 show 200 or less and 650 or more, respectively. In general,
"
playing with" should be a sophisticated process involving hill climbing,
genetic search, simulated annealing, and other fancy strategies for finding the
very best values. In a computer simulation, we'd do that. However, we can do a
reasonable job, for the sake of demonstration, by just tweaking the numbers by
hand in the spreadsheet.
, to find the lowest overall time at which
columns 8 and 9 show 200 or less and 650 or more, respectively. In general,
"
playing with" should be a sophisticated process involving hill climbing,
genetic search, simulated annealing, and other fancy strategies for finding the
very best values. In a computer simulation, we'd do that. However, we can do a
reasonable job, for the sake of demonstration, by just tweaking the numbers by
hand in the spreadsheet.
I have to admit that as I did so, I got kinaesthetic feelings as if I where actually driving. When I 'ran off the track,' that is, picked numbers that gave me x > 200, I gritted my teeth and blushed. When I was still unwinding at the end, I got that panicky feeling of understeer, knowing that I wasn't going to stay on after the end of the segment, and so on.
The best values I found by hand are shown in the following table at r = 167.5, k = 3.25, and kunwind = 7.22. That means that we take 3.25 seconds to bury the gas and 7.22 seconds to unwind the wheel. There are solutions with lower segment times, but, since we're still unwinding long after the segment is done, I reject these solutions as assuming too much about what's going on after our segment is done. With more track to work with, however, we can find lots more time. In fact, it's a slightly surprising fact that by taking 9 seconds to unwind at r = 167.5, k = 3.25, we lose hardly any time and stay 15 feet inside the outer edge. There is quite a bit of territory to investigate even in this simple model.
| r | k | kunwind | Best time Found |
Dummy Time |
Dummy- Best |
Best Total Time Found |
|---|---|---|---|---|---|---|
| 155 | 1.500 | 2.000 | 6.500 | 6.779 | 0.279 | 16.901 |
| 160 | 2.500 | 3.700 | 6.875 | 7.189 | 0.314 | 16.747 |
| 165 | 3.000 | 5.950 | 7.050 | 7.482 | 0.432 | 16.550 |
| 167.5 | 3.250 | 7.22 | 7.120 | 7.605 | 0.485 | 16.466 |
| 170 | 3.500 | 8.550 | 7.225 | 7.716 | 0.491 | 16.433 |
| 175 | 4.000 | 11.170 | 7.400 | 7.912 | 0.512 | 16.367 |
| 180 | 4.500 | 13.330 | 7.575 | 8.082 | 0.507 | 16.337 |
| 185 | 5.000 | 30.000 | 7.700 | 8.233 | 0.533 | 16.282 |
Since the best dummy time, with the widest possible circle, is 16.760, and the best time I found here was 16.466, the improvement by unwinding and accelerating simultaneously is 0.294 seconds. This is very significant. If the exit straight were longer, the improvement would be even more dramatic since it would continue to accumulate time down the straight.
Note that this does not involve changing the entry to the corner other than by slowing down! There is no trail braking or lifting-while-turning or other risk-taking going on at corner entry. There is a very important driving lesson, here: to go faster, it is not necessary to take risks on corner entry. It is, in fact, both safer and faster just to slow down on the entry. The improved exit will follow naturally from the combination of looking far ahead and of being smooth. And that's not even fair!
There is no guarantee that this is the best possible improvement in the model. I found these numbers by 'seat-of-the-pants' tweaking. A more systematic or algorithmic search would very likely find better ones. In other words, I was able to find almost three tenths by just driving a better line without trying very hard at all. There is another driving lesson, here: just driving a better line gives better times time without changing the driver's margin for error, that is, without getting deeper into the g limits of the machine.
For the future, we can start taking more risks to get even more improvement. We can risk accelerating before the apex and we can risk deeper entry by trail braking, that is, easing off the brake and winding up the steering wheel at the same time. These manoeuvres do entail more driver risk since they are new opportunities for loss of car control.
Erratum: in part 17, I wrote " By driving a line just one foot larger than the minimum, one is able to apex more than fifteen degrees later!" . I should have written " …fifteen degrees earlier!" The point was that the tightest line does not apex until the geometric exit of the corner, and that's way too late. The slip-of-the-pen occurred because one is so accustomed to talking about late apexing as preferable.