 |
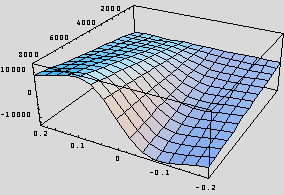 |
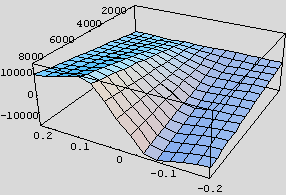
The Magic Formulae (Physics of Racing parts 21, 22, 24, 25) for grip versus slip have some disadvantages for the simulation programmer. Chief among them are the complicated mathematical structure and the large number of parameters. In this instalment, we show a much simpler mathematical expression that mimics the most important, overall features of the Magic Formulae with many fewer parameters. This "Magic Trick" formula is much easier to code and debug, requires much less computing horsepower, and differs by less than 10% almost everywhere from Pajecka: probably sufficiently accurate for gaming simulation. Just to tantalize you, let me offer the following two plots:
 |
 |
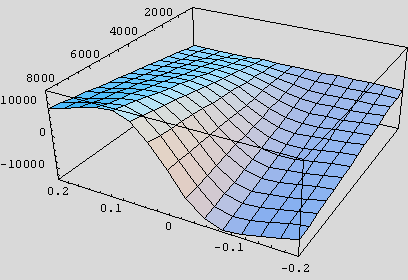
The one on the left is the full, longitudinal Magic Formula from Part 21. The
one on the right is a plot of 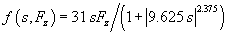 , where s is longitudinal slip and Fz
is vertical load in Newtons, as before. This function is much easier to grasp
and remember than is the Pajecka formula. Also, it is plain to see that the two
plots are so similar that we should expect no gross handling differences were we
to use the right-hand in lieu of the left-hand. In the rest of this instalment,
I detail the methods for obtaining the numerical values of the three parameters.
, where s is longitudinal slip and Fz
is vertical load in Newtons, as before. This function is much easier to grasp
and remember than is the Pajecka formula. Also, it is plain to see that the two
plots are so similar that we should expect no gross handling differences were we
to use the right-hand in lieu of the left-hand. In the rest of this instalment,
I detail the methods for obtaining the numerical values of the three parameters.
The full Magic Formulae were developed for professional research in tyre dynamics. That is why they have so many parameters: they must model everything from large truck tyres to off-road tyres to racing slicks, plus every subtlety of behaviour of every different type of tyre. For simulation and gaming, however, the most important behaviour is simply breakaway instability: the decrease in grip with increasing slip beyond the limits. Minor bumps and wiggles in the curves may be critical to capture differences in brand or type or rubber compound, but they are probably overkill even for detailed simulations like Grand Prix Legends or NASCAR 4. Since the Magic Formulae are "the only game in town," however, simulation programmers tend to use them whilst purposefully wasting their subtle capabilities. In fact, my own presentations of the formulae set most of the parameters to zero value, and mine was derived directly from Genta's (Motor Vehicle Dynamics, pub. World Scientific, 1999). So the available modelling 'dynamic range,' as it were, of the Magic Formulae, seems too large for our applications. We need a simpler formula. After playing around for a little while, I found that the following bears an uncanny resemblance to the Magic Formula, but with only three parameters, (A B, P):
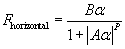
This is just a generic form of the formula, in which Fhorizontal
could be Flateral or Flongitudinal, and 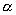 could
be slip angle or slip ratio. In other words, the sketch above can account for
either the longitudinal (part 21) or the lateral Magic Formula (part 22). Let's
analyse the longitudinal formula in detail, using Mathematica (MMA, introduced
in PhoRS part 27). I make reference to the longitudinal formula from part
21 without copying it here, so you will need part 21 on hand to go
forward from this point. You will also need familiarity with Mathematica, and
possibly to have its manual on hand.
could
be slip angle or slip ratio. In other words, the sketch above can account for
either the longitudinal (part 21) or the lateral Magic Formula (part 22). Let's
analyse the longitudinal formula in detail, using Mathematica (MMA, introduced
in PhoRS part 27). I make reference to the longitudinal formula from part
21 without copying it here, so you will need part 21 on hand to go
forward from this point. You will also need familiarity with Mathematica, and
possibly to have its manual on hand.
Encode the Pajecka b parameters twice as vectors, one symbolic, one as numeric rules for Genta's supposed Ferrari:
ClearAll [b] |
So, it's meaningful to do things like this
b[symbolic] /. b[ferrari]
Define some helper functions and more numeric rules (the nomenclature will be obvious if you have one eye on the equations in part 21 this is a straight transcription):
b[n_Integer] := b[symbolic] [[n+1]]
muPeak[fz_] := b[1] fz + b[2]
bigD[fz_] := muPeak[fz] fz
bb0d[fz_] := (b[3] fz2 + b[4] fz) E-b[5]fz
bigB[fz_] := 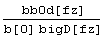
 MegaNewton, KN
MegaNewton, KN KiloNewton,
K
KiloNewton,
K 1000,
1000, 1000, Mega
1000, Mega 1000000,
1000000, 0, 1.
0, 1. 1, -1.
1, -1. 1,
100.
1,
100. 100}
100}
In our numerical exposition of the formula in part 21, we found the constant 0.0822203 popping up over and over. So, test the current forms to see if the same constant appears by substituting the Ferrari's data into them:
Simplify[bigB[aa KN] /. b[ferrari]] /. numRulez
0.0822203
Add more helpers:
bigS[sigma_, fz_] := (100 sigma) + b[9] fz + b[10]
bigE[fz_] := b[6] fz2 + b[7] fz + b[8]
and, finally, the whole formula:
fx[sigma_, fz_ ] := Module[
{SB = bigS[sigma, fz] bigB[fz],
e = bigE[fz],
bigD[fz] Sin[b[0] ArcTan[SB + e (ArcTan[SB] - SB)]]]
Make a version of the formula with the Ferrari substituted in:
fxNum[s_, fz_] := fx[s, fz] / Newton /. b[ferrari] /.
numRulez
Evaluate this final formula symbolically to check against part 21, then numerically, with a big plot:
fxNum[sig, zed]
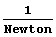 (1.688 zed Sin[
(1.688 zed Sin[
1.65 ArcTan[8.22203 sig - 10. (-8.22203 sig +
ArcTan[8.22203 sig])]])
Plot3D[fxNum[sigma, fz Newton],
{sigma, -.20, .20}, {fz, 1, 8000}, ViewPoint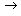 {-1.3,
2.4, 1.5}]
{-1.3,
2.4, 1.5}]
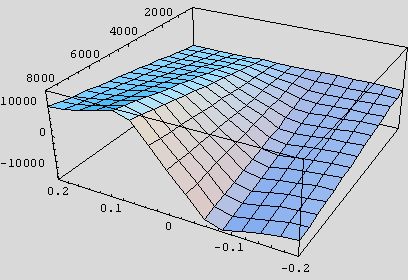
We've successfully reproduced the Magic Formula, and this is the plot we want to emulate. So far, there has been nothing new, just recasting of familiar territory in Mathematica, where we can manipulate the data and formulas. The new function is vastly easier to write down (that's the whole point!), and the plot looks very similar:
fx2Num[s_, fzN_, A_, B_, P_ ] := B fzN s / (1 + Abs[A s]^ P)
Plot3D[fx2Num[sig, fzn, 9.625, 31, 2.375],
{sig, - .20, .20}, {fzn, 1, 8000}, ViewPoint 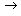 {-1.3,
2.4, 1.5}]
{-1.3,
2.4, 1.5}]
It remains only to show how to obtain the parameter values
(A, B, P) = (9.625, 31.0, 2.375).
The short answer is by the least squares method. The slightly longer answer is to subtract the two plots, sum up the squares of the differences, and then find those values of (A, B, P) that minimize this sum of squares. In the following, I use the already known best values, as if they were handed to me by an oracle. The reason I do this is that it keeps the presentation short: you don't have to look at a bunch of trial-and-error plots gone haywire. But imagine that you don't know the values as I talk you through the process of finding them. I talk you through it because the process is generic, meaning that you can apply it to parameter-searching problems similar to this one.
First, plot the errors, that is, the difference between the two forms.
errdiff1[sig_, fzn_, A_, B_, P_] :=
(fxNum[sig, fzn Newton] - fx2Num[sig, fzn, A, B, P])
Timing[Plot3D[errdiff1[sig, fzn, 9.625, 31, 2.375],
{sig, -.20, .20}, {fzn, 1, 8000}, ViewPoint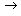 {-1.3,
2.4, 1.5}]]
{-1.3,
2.4, 1.5}]]
{0.812 second, - SurfaceGraphics -}
Note that the maximum magnitude of the errors is about 800 N, or less than 10% of the maximum force. Given that the shape of the plot is very similar to that of Pajecka, hence, that the behavioural characteristics will be similar, we should feel encouraged to go on, with the reservation that the errors are large at the origin, where the force is small. In fact, the errors do reach around 32% at the origin, as shown in the next plots
errpct[sig_, fzn_, A_, B_, P_] :=
100 Abs[(1 - fx2Num[sig, fzn, A, B, P] / fxNum[sig,
fzn Newton])]
TimingPlot[Plot3D[errpct[sig, fzn, 9.625, 31, 2.375],
{sig, -.20, .20}, {fzn, 1, 8000}, ViewPoint 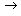 ]]
]]
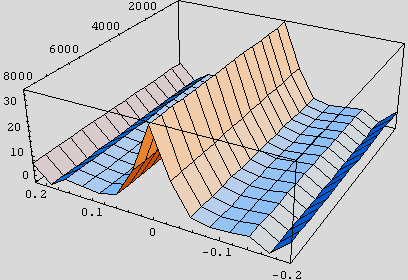
However, this does not concern me very much, for a couple of reasons. First, consider the fact that most authors are satisfied to use a linear approximation near the origin. Witness the ever-present cornering stiffness in the lateral case. Neither of our forms is particularly linear and would probably deviate from a linear approximation at least as much as they deviate from one another. If a linear approximation to Pajecka is good enough, why wouldn't a handy nonlinear approximation, which happens to have much better overall behaviour, be good enough? Secondly, in racing simulation, we are seldom in the linear region, and we should be much more concerned with the differences near the force maxima, around s = 0.15. At these values, the errors are much smaller, well under 10%.
Turning attention back to the plot of errors, notice that some errors are negative and some are positive. That's the reason that we square them: we want the overall sum to be positive for any values of the parameters. We don't want to add negative errors to positive errors and risk getting a low estimate of variance. Note that we might just as well add the absolute values rather than the squares, but squares are much easier to manage symbolically since they are smooth (differentiable) at the origin. Also, squaring errors amounts to an assumption of independence: it treats the errors just like components of a vector in a large-dimensional Euclidean space. Historically, a considerable number of tools were developed to solve such problems analytically (symbolically), so squares it is. In fact, we could approach the present problem symbolically with Mathematica, and we might do that in a later instalment.
For now, in the interest of getting results quickly, we do a brute-force search for the best values of (A, B, P). I like to call this search method archaeological, because it's the same one archaeologists use to search a site for artefacts: grid off the search space, then exhaustively examine each grid cell. Since (A, B, P) spans a three-dimensional space, each cell is a cube, just like a real archaeological dig! Note that archaeological search is dumb: it's much more clever to do hill climbing (steepest descent), simulated annealing, Kernighan-Lin, or symbolic solution. However, precisely because archaeological search is so dumb, it's nearly trivial to code and debug. For many problems, human coding time is more valuable than computer time, and that's the case here. So we let the computer do a bit of extra heavy sweating to save our effort. Note we don't have to do these searches in real time in the simulation: we only have to do one search for each set of Pajecka parameters. If a simulation has 20 different kinds of tyres, 20 searches are done ahead of time and the (A, B, P) parameters go into the simulation in a table. If it were necessary to search in real time, then cleverer methodology and coding would be justified.
First, zoom in on some two-dimensional slices of the search space and see if
we're near a minimum. Look at  , the sum over
, the sum over  from, say, -0.2 to
0.2 by 0.02 and Fz from, say, 1 to 8000 by 500 of the squares
of the errors. Keep the exponent P fixed for this slice and vary A
from 8 to 12 and B from 27 to 37.
from, say, -0.2 to
0.2 by 0.02 and Fz from, say, 1 to 8000 by 500 of the squares
of the errors. Keep the exponent P fixed for this slice and vary A
from 8 to 12 and B from 27 to 37.
s2[A_, B_, P_] := Module[
{v = 0},
Do[v += errdiff2[s, f, A, B, P],
{s, -0.2, 0.2, 0.02}, {f, 1, 8000, 500}]
v]
Timing[Plot3D[s2[i, j, 2.375],
{i, 8, 12}, {j, 27, 37}, ViewPoint {-1.3,
2.4, 1.5}]]
{-1.3,
2.4, 1.5}]]
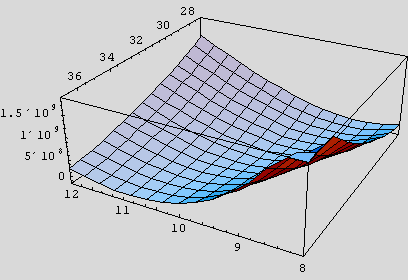
{247.496 Second , - SurfaceGraphics -}
Notice the timing: this plot took some time to produce, so we're having to wait a little for results. More importantly, notice the broad trough at the bottom, suggesting that a minimum can be found in the trough somewhere. A contour plot of the same region gives us even more confidence that we're on the correct archaeological site and can begin digging:
Timing[ContourPlot[s2[i, j, 2.375], {i, 6, 14}, {j, 17,
47}]]
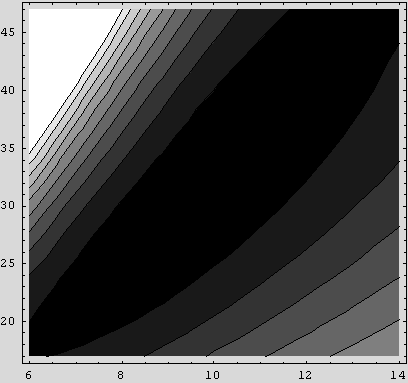
{256.328 Second , - ContourGraphics -}
The contour plot shows that the trough is roughly elliptical and most likely
holds a minimum of 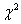 . It is not certain to do, and this business of
parameter searching can be quite hazardous--it's at least as tricky as
integration (part 28). However, for this application, we're almost splitting
hairs. The "Magic Trick" function, by eyeball, looks like an effective
substitute for full Pajecka, for a wide range of (A, B, P)
parameters. We can probably get "close enough" just by eyeball. In
fact, the trough in the plot is quite broad, suggesting that a large range of
values produce almost equally good results. In any event, we should perform a
modicum of due diligence just in the name of professionalism of practice.
. It is not certain to do, and this business of
parameter searching can be quite hazardous--it's at least as tricky as
integration (part 28). However, for this application, we're almost splitting
hairs. The "Magic Trick" function, by eyeball, looks like an effective
substitute for full Pajecka, for a wide range of (A, B, P)
parameters. We can probably get "close enough" just by eyeball. In
fact, the trough in the plot is quite broad, suggesting that a large range of
values produce almost equally good results. In any event, we should perform a
modicum of due diligence just in the name of professionalism of practice.
Look at another slice, this time fixing B.
Timing[Plot3D[s2[i, 31, k],
{i, 9.5, 9.75}, {k, 2.25, 2.5}, ViewPoint {-1.3,
2.4, 1.5}]]
{-1.3,
2.4, 1.5}]]
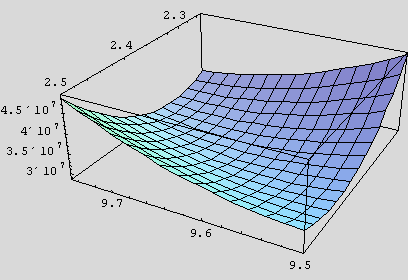
{262.708 Second , - SurfaceGraphics -}
Timing[ContourPlot[s2[i, 31, k], {i, 9.5, 9.75}, {k, 2.25,
2.5}]]
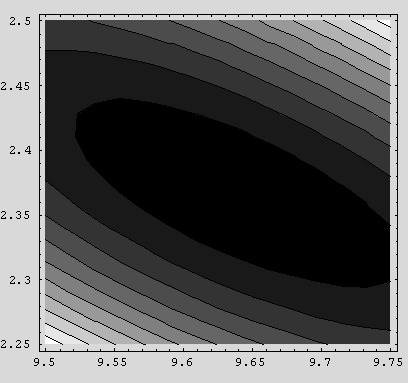
{263.458 Second , - ContourGraphics -}
This slice has almost the same character as the previous one: a broad, narrow
trough that likely contains the minimum of 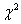 . We are now
fortified with confidence and proceed to search:
. We are now
fortified with confidence and proceed to search:
run[step_, {alo_, ahi_}, {blo_, bhi_}, {plo_, phi_}] :=
Timing[Module[{ax = 0, bx = 0, px = 0,
ebest = $MaxMachineNumber, etest = 0,
abest = 0, bbest = 0, pbest = 0},
Do[
etest = s2[ax, bx, px]
If[etest < ebest, ebest = etest
abest = ax bbest = bx pbest = px
Print[{ebest, abest, bbest, pbest}], Null],
{ax, alo, ahi, step},
{bx, blo, bhi, step},
{px, plo, phi, step}]
{ebest, abest, bbest, pbest}]]
run[1 / 8., {9.5, 9.75}, {30.50, 31.50}, {2.250, 2.5}]
{4.08339 x 107, 9.5, 30.5, 2.25}
{2.90981 x 107, 9.5, 30.5, 2.375}
{2.90128 x 107, 9.625, 30.875, 2.375}
{2.89942 x 107, 9.625, 31., 2.375}
{82.208 Second, {2.89942 x 107, 9.625, 31., 2.375}}
Voila! We have found the promised values (A, B, P) = (9.625, 31.0, 2.375).
Notice how trivial is the searching code: just a triple loop over the
parameter space. However, the embedded function, s2, is,
itself a double loop over the slip s and vertical load Fz,
so we have a quintuple loop. I invite you to experiment with longer-running,
finer-grained searches by varying the first input to run.
The inputs are the search step size and the search boundaries for the three
parameters. All three parameters are stepped by the same increment. I warn you
that as the search grain is made finer, the minimum becomes slippery and the
boundaries of the search have to be adjusted. This is the trial-and-error that I
mentioned at the beginning of the article. It doesn't matter much that we have
an absolute minimum in our application. But, in other applications, this
slipperiness could be critically important and we would be forced to abandon
archaeological search for other methods.